Definisi Fungsi (Pemetaan)

Kembali kita akan belajar matematika. Dan tema bahasan yang akan kita pelajari bersama adalah Definisi Fungsi (Pemetaan). Apakah sobat sudah tahu perbedaan antara fungsi dan relasi? Nah, untuk menjawab pertanyaan tersebut, sobat harus paham dulu definisi dari fungsi (pemetaan) dan apa definisi relasi.

Pada postingan kali ini, kita tidak akan belajar apa itu relasi, namun yang akan kita pelajari kali ini adalah definisi dari fungsi (pemetaan). Agar sobat lebih paham dan mengerti apa itu fungsi, perhatikan penjelasan di bawah ini. Kita juga sudah menyiapkan beberapa contoh soal sebagai bahan acuan buat sobat semua.

Definisi Fungsi (Pemetaan)

Di bawah ini ada contoh table pengambilan data nilai ujian matematika dari enam siswa dari kelas unggulan.

Dari tabel di atas, kita bisa membuat sebuah diagram panah seperti berikut ini.

Gambar yang ada di atas merupakan contoh gambar diagram panah relasi yang diperoleh dari nilai ujian matematika siswa yang tersaji pada tabel di atas. Nah, dari diagram panah tersebut kita bisa menyimpulkan jika :

– Setiap siswa mendapatkan nilai ujian. Hal ini menunjukkan jika setiap anggota A memiliki pasangan atau kawan terhadap anggota B.

– Setiap siswa tepat mendapatkan masing-masing satu nilai. Hal ini menunjukkan jika anggota A memiliki tepat satu pasangan atau kawan terhadap anggota B, namun anggota B bisa memilih lebih dari satu pasangan anggota A.

Dari uraian di atas apa yang sobat dapat simpulkan? Kesimpulan yang bisa kita ambil adalah relasi dari himpunan A – himpunan B merupakan relasi fungsi atau pemetaan dimana setiap anggota A di pasangkan tepat satu-satu terhadap anggota B.

Dari sini kita juga bisa menyimpulkan jika suatu relasi dikatakan sebuah fungsi jika memenuhi dua syarat yakni yang pertama adalah setiap anggota A memiliki pasangan di anggota B. Namun apabila salah satu dari anggota A tidak memiliki pasangan terhadap anggota B, maka bisa dikatakan relasi tersebut bukan termasuk fungsi. Dan syarat yang kedua adalah setiap anggota A dipasangkan tepat satu-satu terhadap anggota B. Dengan kata lain anggota A tidak boleh memiliki pasangan anggota B lebih dari satu. Namun untuk syarat yang kedua ini tidak berlaku untuk pasangan sebaliknya dalam artian jika syarat yang pertama telah terpenuhi, maka anggota B boleh memiliki lebih dari satu pasangan dari anggota A.

Untuk membantu sobat bangkusekolah.com lebih paham akan definisi fungsi atau pemetaan, pahami contoh soal yang ada di bawah ini.

Contoh Soal

Coba kalian perhatikan gambar yang ada di bawah ini.
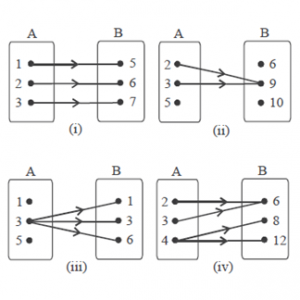Dari diagram-diagram panah di atas, diagram yang manakah yang merupakan diagram panah fungsi? Dan berikan alasannya.
Jawab :

Nah, untuk menjawab contoh soal di atas, kita terlebih dahulu harus paham dengan syarat dari suatu relasi yang bisa dikatakan sebuah fungsi.

(i). Dikatakan sebuah fungsi jika setiap anggota A memiliki satu pasangan terhadap anggota B

(ii). Dikatakan bukan sebuah fungsi jika ada salah satu anggota A tidak memiliki pasangan terhadap anggota B

(iii). Dikatakan bukan sebuah fungsi jika ada anggota A tidak memiliki pasangan anggota B serta ada salah satu dari anggota A yang mempunya pasangan anggota B lebih dari satu

(iv). Dan dikatakan bukan sebuah fungsi jika adalah satu satu dari anggota A memiliki lebih dari satu pasangan anggota B

Dari contoh soal di atas, apa kalian sudah bisa membedakan yang mana relasi dan yang mana fungsi? Ok sampai disini perjumpaan kita. Semoga bisa berguna bagi sobat semua.